Symbolic Regression

Objective

This academic project focuses on developing a reduced-order model for the 1D advection-diffusion PDE with Gaussian initial conditions. By combining convolutional autoencoders for dimensionality reduction and SINDy-like symbolic regression for interpretable decoding, the work aims to create efficient, interpretable surrogates for PDE simulations, alleviating computational burdens in parameter exploration.

Key Components

1. Mathematical Formulation

The advection-diffusion equation is formulated in both conservative and non-conservative forms, with a Gaussian initial condition \(u(x, 0) = \frac{1}{\sigma_0 \sqrt{2\pi}} \exp\left(-\frac{(x-\mu_0)^2}{2\sigma_0^2}\right)\).

Analytical solutions assume Gaussian preservation, reducing to ODEs for mean \(\mu(t)\) and variance \(\sigma^2(t)\).

2. Numerical Solver

Spatial: Upwind for advection, centered finite difference for diffusion. Temporal: Explicit Euler. Stability via CFL and diffusion conditions.

3. Data Generation

Vary initial parameters \(\mu_0 \in [0.3, 0.5, 0.7]\) and \(\sigma_0 \in [0.05, 0.1, 0.15]\) on domain [0,1] with \(N_x = 96\), \(a=1\), \(D=0.1\), generating thousands of snapshots.

4. Convolutional Autoencoder

A PyTorch-based autoencoder compresses 1D snapshots to 2D latent space using Conv1D layers (encoder) and ConvTranspose1D (decoder), trained with MSE loss and Adam optimizer.

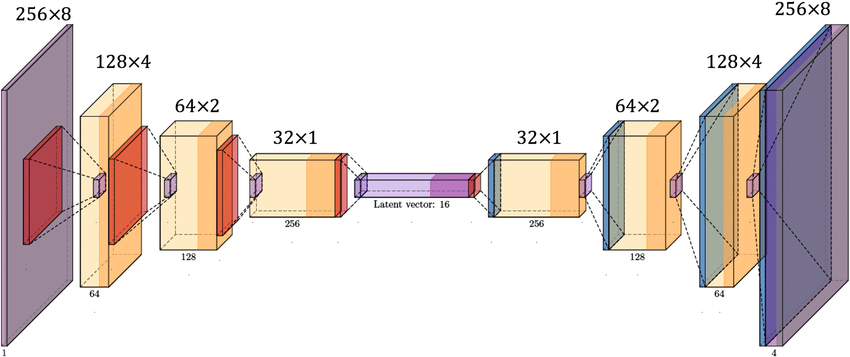
5. Symbolic Decoder (SINDy-Like)

Post-encoding, a linear combination of basis functions (polynomials, trig, exp) with L1 regularization learns sparse mappings from latent vectors to PDE states.

Results

Autoencoder and SINDy Performance

The autoencoder achieves low MSE (<1e-3), with reconstructions nearly matching ground truth.

SINDy decoder, trained over 10,000 epochs, yields sparse expressions approximating snapshots well.

Impact and Future Work

This hybrid approach enhances PDE modeling by combining neural efficiency with symbolic interpretability, suitable for real-time applications. Prospects include extending to higher dimensions, refining function libraries, embedding PDE knowledge, and enabling real-time control.

Download the project report here.

Download the project presentation here.